我的下一行 Code

The Derivative of The Common Model

May 01, 2023

Introduction

In this post, I'm going to show you how to derivative the following common mathematical model:

  • Polynomials Function
  • Power Function
  • Exponential Function
  • Logarithmic Function
  • Trigonometric Function
  • Inverse Trigonometric Function

And why we need to the Antiderivative.

Essential Rules

The Constant Multiple Rule

ddx(c⋅f(x))=c⋅ddxf(x)\frac{d}{dx}(c \cdot f(x)) = c \cdot \frac{d}{dx} f(x)

The Sum Rule

ddx(f(x)+g(x))=ddxf(x)+ddxg(x)\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}f(x) + \frac{d}{dx}g(x)

The Difference Rule

ddx(f(x)−g(x))=ddxf(x)−ddxg(x)\frac{d}{dx}(f(x) - g(x)) = \frac{d}{dx}f(x) - \frac{d}{dx}g(x)

The Product Rule

ddx(f(x)⋅g(x))=ddx(f(x))⋅g(x)+f(x)⋅ddx(g(x))\frac{d}{dx}(f(x) \cdot g(x)) = \frac{d}{dx}(f(x)) \cdot g(x) + f(x) \cdot \frac{d}{dx}(g(x))
Proof
F(x)=f(x)⋅g(x)ddx(F(x))=lim⁡Δx→0F(x+Δx)−F(x)ΔxF(x+Δx)−F(x)=f(x+Δx)⋅g(x+Δx)−f(x)⋅g(x)=f(x+Δx)⋅g(x+Δx)−f(x)⋅g(x+Δx)+f(x)⋅g(x+Δx)−f(x)⋅g(x)=(f(x+Δx)−f(x))⋅g(x+Δx)+f(x)⋅(g(x+Δx)−g(x))F′(x)=lim⁡Δx→0F(x+Δx)−F(x)Δx=lim⁡Δx→0(f(x+Δx)−f(x))⋅g(x+Δx)+f(x)⋅(g(x+Δx)−g(x))Δx=lim⁡Δx→0(f(x+Δx)−f(x))⋅g(x+Δx)Δx+lim⁡Δx→0f(x)⋅(g(x+Δx)−g(x))Δx=lim⁡Δx→0f(x+Δx)−f(x)Δx⋅g(x+Δx)+lim⁡Δx→0f(x)⋅g(x+Δx)−g(x)Δx=lim⁡Δx→0f(x+Δx)−f(x)Δx⋅lim⁡Δx→0g(x+Δx)+lim⁡Δx→0f(x)⋅lim⁡Δx→0g(x+Δx)−g(x)Δx=ddx(f(x))⋅g(x)+f(x)⋅ddx(g(x))\begin{aligned} F(x) &= f(x) \cdot g(x) \\[10pt] \frac{d}{dx}(F(x)) &= \lim\limits_{\Delta x \to 0} \frac{F(x + \Delta x) - F(x)}{\Delta x} \\[10pt] F(x + {\Delta x}) - F(x) &= f(x + \Delta x) \cdot g(x + \Delta x) - f(x) \cdot g(x) \\[10pt] &= f(x + \Delta x) \cdot g(x + \Delta x) - f(x) \cdot g(x + \Delta x) + f(x) \cdot g(x + \Delta x) - f(x) \cdot g(x) \\[10pt] &= (f(x + \Delta x) - f(x)) \cdot g(x + \Delta x) + f(x) \cdot (g(x + \Delta x) - g(x)) \\[10pt] F'(x) &= \lim\limits_{\Delta x \to 0} \frac{F(x + \Delta x) - F(x)}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{(f(x + \Delta x) - f(x)) \cdot g(x + \Delta x) + f(x) \cdot (g(x + \Delta x) - g(x))}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{(f(x + \Delta x) - f(x)) \cdot g(x + \Delta x)}{\Delta x} + \lim\limits_{\Delta x \to 0} \frac{f(x) \cdot (g(x + \Delta x) - g(x))}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \cdot g(x + \Delta x) + \lim\limits_{\Delta x \to 0} f(x) \cdot \frac{g(x + \Delta x) - g(x)}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \cdot \lim\limits_{\Delta x \to 0} g(x + \Delta x) + \lim\limits_{\Delta x \to 0} f(x) \cdot \lim\limits_{\Delta x \to 0} \frac{g(x + \Delta x) - g(x)}{\Delta x} \\[10pt] &= \frac{d}{dx}(f(x)) \cdot g(x) + f(x) \cdot \frac{d}{dx}(g(x)) \\[10pt] \end{aligned}

The Quotient Rule

(f(x)g(x))′=f′(x)⋅g(x)−f(x)⋅g′(x)(g(x))2,g(x)≠0(\frac{f(x)}{g(x)})' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}, \quad g(x) \neq 0
Proof
F(x)=f(x)g(x),g(x)≠0F′(x)=lim⁡Δx→0F(x+Δx)−F(x)ΔxF(x+Δx)−F(x)=f(x+Δx)g(x+Δx)−f(x)g(x)=f(x+Δx)⋅g(x)−f(x)⋅ g(x+Δx)g(x+Δx)⋅ g(x)F′(x)=lim⁡Δx→0f(x+Δx)⋅g(x)−f(x)⋅ g(x+Δx)g(x+Δx)⋅ g(x)⋅Δx=lim⁡Δx→0f(x+Δx)⋅g(x)−f(x)⋅ g(x+Δx)Δx⋅lim⁡Δx→01g(x+Δx)⋅ g(x)=H(x)⋅G(x)\begin{align*} F(x) &= \frac{f(x)}{g(x)}, \quad g(x) \neq 0 \\[10pt] F'(x) &= \lim\limits_{\Delta x \to 0} \frac{F(x + \Delta x) - F(x)}{\Delta x} \\[10pt] F(x + {\Delta x}) - F(x) &= \frac{f(x + \Delta x)}{g(x + \Delta x)} - \frac{f(x)}{g(x)} \\[10pt] &= \frac{f(x + \Delta x) \cdot g(x) - f(x) \cdot \ g(x + \Delta x) }{g(x + \Delta x) \cdot \ g(x)} \\[10pt] F'(x) &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) \cdot g(x) - f(x) \cdot \ g(x + \Delta x)} {g(x + \Delta x) \cdot \ g(x) \cdot \Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) \cdot g(x) - f(x) \cdot \ g(x + \Delta x)}{\Delta x} \cdot \lim\limits_{\Delta x \to 0} \frac{1}{g(x + \Delta x) \cdot \ g(x)} \\[10pt] &= H(x) \cdot G(x) \end{align*}
H(x)=lim⁡Δx→0f(x+Δx)⋅g(x)−f(x)⋅g(x)+f(x)⋅g(x)−f(x)⋅ g(x+Δx)Δx=lim⁡Δx→0f(x+Δx)⋅g(x)−f(x)⋅g(x)−(f(x)⋅ g(x+Δx)−f(x)⋅g(x))Δx=lim⁡Δx→0f(x+Δx)⋅g(x)−f(x)⋅g(x)Δx−lim⁡Δx→0f(x)⋅ g(x+Δx)−f(x)⋅g(x)Δx=(lim⁡Δx→0f(x+Δx)−f(x)Δx)⋅g(x)−f(x)⋅(lim⁡Δx→0g(x+Δx)−g(x)Δx)=f′(x)⋅g(x)−f(x)⋅g′(x)\begin{align*} H(x) &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) \cdot g(x) - f(x) \cdot g(x) + f(x) \cdot g(x) - f(x) \cdot \ g(x + \Delta x)}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) \cdot g(x) - f(x) \cdot g(x) - (f(x) \cdot \ g(x + \Delta x) - f(x) \cdot g(x))}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) \cdot g(x) - f(x) \cdot g(x)}{\Delta x} - \lim\limits_{\Delta x \to 0} \frac{f(x) \cdot \ g(x + \Delta x) - f(x) \cdot g(x)}{\Delta x} \\[10pt] &= (\lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}) \cdot g(x) - f(x) \cdot (\lim\limits_{\Delta x \to 0} \frac{g(x + \Delta x) - g(x)}{\Delta x}) \\[10pt] &= f'(x) \cdot g(x) - f(x) \cdot g'(x) \\[10pt] \end{align*}
G(x)=lim⁡Δx→01g(x+Δx)⋅ g(x)=1g(x)⋅lim⁡Δx→01g(x+Δx)=1g(x)⋅1g(x)=1(g(x))2,g(x)≠0\begin{align*} G(x) &= \lim\limits_{\Delta x \to 0} \frac{1}{g(x + \Delta x) \cdot \ g(x)} \\[10pt] &= \frac{1}{g(x)} \cdot \lim\limits_{\Delta x \to 0} \frac{1}{g(x + \Delta x)} \\[10pt] &= \frac{1}{g(x)} \cdot \frac{1}{g(x)} \\[10pt] &= \frac{1}{(g(x))^2}, \quad g(x) \neq 0 \\[10pt] \end{align*}
F′(x)=H(x)⋅G(x)=(f′(x)⋅g(x)−f(x)⋅g′(x))⋅1(g(x))2=f′(x)⋅g(x)−f(x)⋅g′(x)(g(x))2 ,g(x)≠0\begin{align*} F'(x) &= H(x) \cdot G(x) \\[10pt] &= (f'(x) \cdot g(x) - f(x) \cdot g'(x)) \cdot \frac{1}{(g(x))^2} \\[10pt] &= \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2} \: , \quad g(x) \neq 0 \\[10pt] \end{align*}

The Chain Rule

ddx(f(h(x)))=ddh(f(h))⋅ddx(h(x))\frac{d}{dx}{(f(h(x)))} = \frac{d}{dh}(f(h)) \cdot \frac{d}{dx}(h(x))
Proof
ddx(f(h(x)))=lim⁡Δx→0ΔfΔx=lim⁡Δx→0ΔfΔh⋅ΔhΔx ,Δh≠0=lim⁡Δh→0ΔfΔh⋅lim⁡Δx→0ΔhΔx=ddh(f(h))⋅ddx(h(x))\begin{align*} \frac{d}{dx}{(f(h(x)))} &= \lim\limits_{\Delta x \to 0} \frac{\Delta f}{\Delta x} \\[10pt] &= \lim\limits_{\Delta x \to 0} \frac{\Delta f}{\Delta h} \cdot \frac{\Delta h}{\Delta x} \text{ ,} \quad \Delta h \neq 0 \\[10pt] &= \lim\limits_{\Delta h \to 0} \frac{\Delta f}{\Delta h} \cdot \lim\limits_{\Delta x \to 0} \frac{\Delta h}{\Delta x} \\[10pt] &= \frac{d}{dh}(f(h)) \cdot \frac{d}{dx}(h(x)) \\[10pt] \end{align*}

Constant Function

f(x)=c, c is a constantf(x) = c, \text{ c is a constant}

Derivative

ddx(f(x))=ddx(c)=0, c is a constant\frac{d}{dx} (f(x)) = \frac{d}{dx}(c) = 0, \text{ c is a constant}
Proof
ddx(f(x))=lim⁡h→0f(x+h)−f(x)hddx(c)=lim⁡h→0c−ch=(c−c)⋅lim⁡h→01h=0⋅lim⁡h→01h=0\begin{aligned} \frac{d}{dx}(f(x)) &= \lim\limits_{h \to 0} \frac{f(x + h) - f(x)}{h} \\[10pt] \frac{d}{dx}(c) &= \lim\limits_{h \to 0} \frac{c - c}{h} \\[10pt] &= (c - c) \cdot \lim\limits_{h \to 0} \frac{1}{h} \\[10pt] &= 0 \cdot \lim\limits_{h \to 0} \frac{1}{h} \\[10pt] &= 0 \end{aligned}

Polynomials Function

f(x)=cnxn+cn−1xn−1+...+c1x+c0f(x) = c_nx^n + c_{n-1}x^{n-1} + ... + c_1x + c_0

Power Function

f(x)=xaf(x) = x^a, aa is a scalar

ddx(xa)=a⋅xa−1\frac{d}{dx}(x^a) = a \cdot x^{a-1}

Exponential Functions

f(x)=axf(x) = a^x, aa is a scalar

ddx(ax)=ax⋅ln(a)\frac{d}{dx}(a^x) = a^x \cdot ln(a)

Proof:

ddx(ax)=ddx(e(ln(a))⋅x)=ddx(e(ln(a))⋅x)⋅ddx(ln(a)⋅x)=e(ln(a))⋅x⋅ln(a)=ax⋅ln(a)\begin{aligned} \frac{d}{dx}(a^x) &= \frac{d}{dx}(e^{(ln(a)) \cdot x}) \\[10pt] &= \frac{d}{dx}(e^{(ln(a)) \cdot x}) \cdot \frac{d}{dx}(ln(a) \cdot x) \\[10pt] &= e^{(ln(a)) \cdot x} \cdot ln(a) \\[10pt] &= a^x \cdot ln(a) \end{aligned}

Natural Exponential Function

f(x)=exddx(ex)=ex\begin{aligned} f(x) &= e^x \\ \frac{d}{dx}(e^x) &= e^x \end{aligned}

Limit of ee

e=lim⁡x→0(1+x)1x=lim⁡n→∞(1+1n)nex=lim⁡n→∞(1+xn)n,x>0\begin{aligned} e &= \lim\limits_{x \to 0}(1 + x)^{\frac{1}{x}} \\[10pt] &= \lim\limits_{n \to \infty}(1 + \frac{1}{n})^n \\[10pt] e^x &= \lim\limits_{n \to \infty}(1 + \frac{x}{n})^n, x > 0 \\[10pt] \end{aligned}

Logarithmic Functions

f(x)=loga(x)ddx(loga(x))=1x⋅ln(a)\begin{aligned} f(x) &= log_a(x) \\[10pt] \frac{d}{dx}(log_a(x)) &= \frac{1}{x \cdot ln(a)} \\[10pt] \end{aligned}

Proof by Implicit Differentiation

y=loga(x)ay=xddx(ay)=ddx(x)ln(a)⋅ay⋅dydx=1dydx=1ln(a)⋅ay=1ln(a)⋅x\begin{aligned} y &= log_a(x) \\[10pt] a^y &= x \\[10pt] \frac{d}{dx}(a^y) &= \frac{d}{dx}(x) \\[10pt] ln(a) \cdot a^y \cdot \frac{dy}{dx} &= 1 \\[10pt] \frac{dy}{dx} &= \frac{1}{ln(a) \cdot a^y} = \frac{1}{ln(a) \cdot x} \\[10pt] \end{aligned}

Natural Logarithmic Function

f(x)=loge(x)=ln(x)ddx(ln(x))=1x\begin{aligned} f(x) &= log_e(x) = ln(x) \\[10pt] \frac{d}{dx}(ln(x)) &= \frac{1}{x} \\[10pt] \end{aligned}

Trigonometric Functions

Review

lim⁡θ→0sin(θ)θ=1lim⁡θ→0cos(θ)−1θ=0sin(x+h)=sin(x)⋅cos(h)+cos(x)⋅sin(h)cos(x+h)=cos(x)⋅cos(h)−sin(x)⋅sin(h)\begin{aligned} \lim\limits_{\theta \to 0}\frac{sin(\theta)}{\theta} &= 1 \\[10pt] \lim\limits_{\theta \to 0}\frac{cos(\theta) - 1}{\theta} &= 0 \\[10pt] sin(x + h) &= sin(x) \cdot cos(h) + cos(x) \cdot sin(h) \\[10pt] cos(x + h) &= cos(x) \cdot cos(h) - sin(x) \cdot sin(h) \\[10pt] \end{aligned}
sin2(θ)+cos2(θ)=1tan2(θ)+1=sec2(θ)1+cot2(θ)=csc2(θ)\begin{aligned} sin^2(\theta) + cos^2(\theta) &= 1 \\[10pt] tan^2(\theta) + 1 &= sec^2(\theta) \\[10pt] 1 + cot^2(\theta) &= csc^2(\theta) \\[10pt] \end{aligned}

Sine Function

sin(θ)=oppositehypotenuseddx(sin(x))=cos(x)\begin{aligned} sin(\theta) &= \frac{opposite}{hypotenuse} \\[10pt] \frac{d}{dx}(sin(x)) &= cos(x) \\[10pt] \end{aligned}
Proof by Definitionddx(f(x))=lim⁡h→0f(x+h)−f(x)hddx(sin(x))=lim⁡h→0sin(x+h)−sin(x)h=lim⁡h→0sin(x)⋅cos(h)+cos(x)⋅sin(h)−sin(x)h=lim⁡h→0sin(x)⋅(cos(h)−1)+cos(x)⋅sin(h)h=sin(x)⋅lim⁡h→0cos(h)−1h+cos(x)⋅lim⁡h→0sin(h)h=sin(x)⋅0+cos(x)⋅1=cos(x)\begin{aligned} \textbf{Proof by Definition} \\[10pt] \frac{d}{dx}(f(x)) &= \lim\limits_{h \to 0}\frac{f(x + h) - f(x)}{h} \\[10pt] \frac{d}{dx}(sin(x)) &= \lim\limits_{h \to 0}\frac{sin(x + h) - sin(x)}{h} \\[10pt] &= \lim\limits_{h \to 0}\frac{sin(x) \cdot cos(h) + cos(x) \cdot sin(h) - sin(x)}{h} \\[10pt] &= \lim\limits_{h \to 0}\frac{sin(x) \cdot (cos(h) - 1) + cos(x) \cdot sin(h)}{h} \\[10pt] &= sin(x) \cdot \lim\limits_{h \to 0}\frac{cos(h) - 1}{h} + cos(x) \cdot \lim\limits_{h \to 0}\frac{sin(h)}{h} \\[10pt] &= sin(x) \cdot 0 + cos(x) \cdot 1 \\[10pt] &= cos(x) \\[10pt] \end{aligned}

Cosine Function

cos(θ)=adjacenthypotenuseddx(cos(x))=−sin(x)\begin{aligned} cos(\theta) &= \frac{adjacent}{hypotenuse} \\ \frac{d}{dx}(cos(x)) &= -sin(x) \end{aligned}
Proof by Definitionddx(f(x))=lim⁡h→0f(x+h)−f(x)hddx(cos(x))=lim⁡h→0cos(x+h)−cos(x)h=lim⁡h→0cos(x)⋅cos(h)−sin(x)⋅sin(h)−cos(x)h=lim⁡h→0cos(x)⋅(cos(h)−1)−sin(x)⋅sin(h)h=cos(x)⋅lim⁡h→0cos(h)−1h−sin(x)⋅lim⁡h→0sin(h)h=cos(x)⋅0−sin(x)⋅1=−sin(x)\begin{aligned} \textbf{Proof by Definition} \\ \frac{d}{dx}(f(x)) &= \lim\limits_{h \to 0}\frac{f(x + h) - f(x)}{h} \\ \frac{d}{dx}(cos(x)) &= \lim\limits_{h \to 0}\frac{cos(x + h) - cos(x)}{h} \\ &= \lim\limits_{h \to 0}\frac{cos(x) \cdot cos(h) - sin(x) \cdot sin(h)- cos(x)}{h} \\ &= \lim\limits_{h \to 0}\frac{cos(x) \cdot (cos(h) - 1) - sin(x) \cdot sin(h)}{h} \\ &= cos(x) \cdot \lim\limits_{h \to 0}\frac{cos(h) - 1}{h} - sin(x) \cdot \lim\limits_{h \to 0}\frac{sin(h)}{h} \\ &= cos(x) \cdot 0 - sin(x) \cdot 1 \\ &= -sin(x) \end{aligned}

Tangent Function

tan(θ)=oppositeadjacent=sin(θ)cos(θ)ddx(tan(x))=sec2(x)\begin{aligned} tan(\theta) &= \frac{opposite}{adjacent} = \frac{sin(\theta)}{cos(\theta)} \\ \frac{d}{dx}(tan(x)) &= sec^2(x) \end{aligned}
Proof by Quotient Ruleddx(tan(x))=ddx(sin(x)cos(x))=ddx(sin(x))⋅cos(x)−sin(x)⋅ddx(cos(x))(cos(x))2=cos(x)⋅cos(x)−sin(x)⋅−sin(x)cos2(x)=cos(x)⋅cos(x)+sin(x)⋅sin(x)cos2(x)=cos2(x)+sin2(x)cos2(x)=1cos2(x)=(1cos(x))2=(sec(x))2=sec2(x)\begin{aligned} \textbf{Proof by Quotient Rule} \\ \frac{d}{dx}(tan(x)) &= \frac{d}{dx}(\frac{sin(x)}{cos(x)}) \\ &= \frac{\frac{d}{dx}(sin(x)) \cdot cos(x) - sin(x) \cdot \frac{d}{dx}(cos(x))}{(cos(x))^2} \\ &= \frac{cos(x) \cdot cos(x) - sin(x) \cdot -sin(x)}{cos^2(x)} \\ &= \frac{cos(x) \cdot cos(x) + sin(x) \cdot sin(x)}{cos^2(x)} \\ &= \frac{cos^2(x) + sin^2(x)}{cos^2(x)} \\ &= \frac{1}{cos^2(x)} \\ &= (\frac{1}{cos(x)})^2 \\ &= (sec(x))^2 \\ &= sec^2(x) \end{aligned}

Cotangent Function

cot(θ)=1tan(θ)ddx(cot(x))=−csc2(x)\begin{aligned} cot(\theta) &= \frac{1}{tan(\theta)} \\ \frac{d}{dx}(cot(x)) &= -csc^2(x) \end{aligned}
Proof by Quotient Ruleddx(cot(x))=ddx(cos(x)sin(x))=ddx(cos(x))⋅sin(x)−cos(x)⋅ddx(sin(x))(sin(x))2=−sin(x)⋅sin(x)−cos(x)⋅cos(x)sin2(x)=−(sin(x)⋅sin(x)+cos(x)⋅cos(x))sin2(x)=−(sin2(x)+cos2(x))sin2(x)=−1sin2(x)=−(1sin(x))2=−(csc(x))2=−csc2(x)\begin{aligned} \textbf{Proof by Quotient Rule} \\ \frac{d}{dx}(cot(x)) &= \frac{d}{dx}(\frac{cos(x)}{sin(x)}) \\ &= \frac{\frac{d}{dx}(cos(x)) \cdot sin(x) - cos(x) \cdot \frac{d}{dx}(sin(x))}{(sin(x))^2} \\ &= \frac{-sin(x) \cdot sin(x) - cos(x) \cdot cos(x)}{sin^2(x)} \\ &= \frac{-(sin(x) \cdot sin(x) + cos(x) \cdot cos(x))}{sin^2(x)} \\ &= \frac{-(sin^2(x) + cos^2(x))}{sin^2(x)} \\ &= -\frac{1}{sin^2(x)} \\ &= -(\frac{1}{sin(x)})^2 \\ &= -(csc(x))^2 \\ &= -csc^2(x) \end{aligned}

Secant Function

sec(θ)=1cos(θ)ddx(sec(x))=tan(x)⋅sec(x)\begin{aligned} sec(\theta) &= \frac{1}{cos(\theta)} \\ \frac{d}{dx}(sec(x)) &= tan(x) \cdot sec(x) \\ \end{aligned}
Proof by Quotient Ruleddx(sec(x))=ddx(1cos(x))=ddx(1)⋅cos(x)−1⋅ddx(cos(x))(cos(x))2=0⋅cos(x)−1⋅−sin(x)(cos(x))2=sin(x)cos2(x)=sin(x)cos(x)⋅1cos(x)=tan(x)⋅sec(x)\begin{aligned} \textbf{Proof by Quotient Rule} \\ \frac{d}{dx}(sec(x)) &= \frac{d}{dx}(\frac{1}{cos(x)}) \\ &= \frac{\frac{d}{dx}(1) \cdot cos(x) - 1 \cdot \frac{d}{dx}(cos(x))}{(cos(x))^2} \\ &= \frac{0 \cdot cos(x) - 1 \cdot -sin(x)}{(cos(x))^2} \\ &= \frac{sin(x)}{cos^2(x)} \\ &= \frac{sin(x)}{cos(x)} \cdot \frac{1}{cos(x)} \\ &= tan(x) \cdot sec(x) \end{aligned}

Cosecant Function

csc(θ)=1sin(θ)ddx(csc(x))=−cot(x)⋅csc(x)\begin{aligned} csc(\theta) &= \frac{1}{sin(\theta)} \\ \frac{d}{dx}(csc(x)) &= -cot(x) \cdot csc(x) \\ \end{aligned}
Proof by Quotient Ruleddx(csc(x))=ddx(1sin(x))=ddx(1)⋅sin(x)−1⋅ddx(sin(x))(sin(x))2=0⋅cos(x)−1⋅cos(x)(sin(x))2=−cos(x)sin2(x)=−cos(x)sin(x)⋅1sin(x)=−cot(x)⋅csc(x)\begin{aligned} \textbf{Proof by Quotient Rule} \\ \frac{d}{dx}(csc(x)) &= \frac{d}{dx}(\frac{1}{sin(x)}) \\ &= \frac{\frac{d}{dx}(1) \cdot sin(x) - 1 \cdot \frac{d}{dx}(sin(x))}{(sin(x))^2} \\ &= \frac{0 \cdot cos(x) - 1 \cdot cos(x)}{(sin(x))^2} \\ &= \frac{-cos(x)}{sin^2(x)} \\ &= \frac{-cos(x)}{sin(x)} \cdot \frac{1}{sin(x)} \\ &= -cot(x) \cdot csc(x) \end{aligned}

Inverse Trigonometric Functions

Derivative of Inverse Sine Function

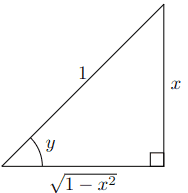
ddx(sin−1(x))=11−x2\frac{d}{dx}(sin^{-1}(x)) = \frac{1}{\sqrt{1 - x^2}}
Proofy=sin−1(x)⇔sin(y)=x=x1=oppositehypotenuse⇒cos(y)=1−x21=adjacenthypotenuse\textbf{Proof} \\ y = sin^{-1}(x) \Leftrightarrow sin(y) = x = \frac{x}{1} = \frac{opposite}{hypotenuse} \Rightarrow cos(y) = \frac{\sqrt{1 - x^2}}{1} = \frac{adjacent}{hypotenuse}

inverse sine triangle

sin(y)=x1cos(y)⋅dydx=1(Implicit Differentiation)dydx=1cos(y)dydx=11−x2ddx(sin−1(x))=11−x2\begin{aligned} sin(y) &= \frac{x}{1} \\[10pt] cos(y) \cdot \frac{dy}{dx} &= 1 \quad \textit{(Implicit Differentiation)} \\[10pt] \frac{dy}{dx} &= \frac{1}{cos(y)} \\[10pt] \frac{dy}{dx} &= \frac{1}{\sqrt{1 - x^2}} \\[10pt] \frac{d}{dx}(sin^{-1}(x)) &= \frac{1}{\sqrt{1 - x^2}} \\[10pt] \end{aligned}

Derivative of Inverse Cosine Function

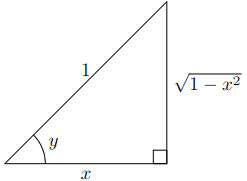
ddx(cos−1(x))=−11−x2\frac{d}{dx}(cos^{-1}(x)) = -\frac{1}{\sqrt{1 - x^2}}
Proofy=cos−1(x)⇔cos(y)=x=x1=adjacenthypotenuse⇒sin(y)=1−x21=oppositehypotenuse\textbf{Proof} \\ y = cos^{-1}(x) \Leftrightarrow cos(y) = x = \frac{x}{1} = \frac{adjacent}{hypotenuse} \Rightarrow sin(y) = \frac{\sqrt{1 - x^2}}{1} = \frac{opposite}{hypotenuse}

inverse cosine triangle

cos(y)=x1−sin(y)⋅dydx=1(Implicit Differentiation)dydx=−1sin(y)dydx=−11−x2ddx(cos−1(x))=−11−x2\begin{aligned} cos(y) &= \frac{x}{1} \\ -sin(y) \cdot \frac{dy}{dx} &= 1 \quad \textit{(Implicit Differentiation)} \\ \frac{dy}{dx} &= - \frac{1}{sin(y)} \\ \frac{dy}{dx} &= - \frac{1}{\sqrt{1 - x^2}} \\ \frac{d}{dx}(cos^{-1}(x)) &= -\frac{1}{\sqrt{1 - x^2}} \\ \end{aligned}

Derivative of Inverse Tangent Function

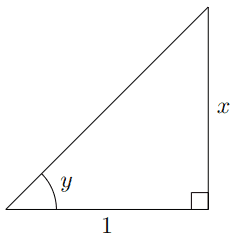
ddx(tan−1(x))=11+x2\frac{d}{dx}(tan^{-1}(x)) = \frac{1}{1 + x^2}
Proofy=tan−1(x)⇔tan(y)=x=x1=oppositeadjacent\textbf{Proof} \\ y = tan^{-1}(x) \Leftrightarrow tan(y) = x = \frac{x}{1} = \frac{opposite}{adjacent}

inverse tangent triangle

tan(y)=xsec2(y)⋅dydx=1(Implicit Differentiation)dydx=1sec2(y)dydx=11+tan2(y)ddx(tan−1(x))=11+x2\begin{aligned} tan(y) &= x \\ sec^2(y) \cdot \frac{dy}{dx} &= 1 \quad \textit{(Implicit Differentiation)} \\ \frac{dy}{dx} &= \frac{1}{sec^2(y)} \\ \frac{dy}{dx} &= \frac{1}{1 + tan^2(y)} \\ \frac{d}{dx}(tan^{-1}(x)) &= \frac{1}{1 + x^2} \\ \end{aligned}

Derivative of Inverse Cotangent Function

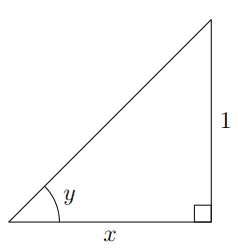
ddx(cot−1(x))=−11+x2\frac{d}{dx}(cot^{-1}(x)) = -\frac{1}{1 + x^2}
Proofy=cot−1(x)⇔cot(y)=x=x1=adjacentopposite\textbf{Proof} \\ y = cot^{-1}(x) \Leftrightarrow cot(y) = x = \frac{x}{1} = \frac{adjacent}{opposite}

inverse cotangent triangle

cot(y)=x−csc2(y)⋅dydx=1(Implicit Differentiation)dydx=−1csc2(y)dydx=−11+cot2(y)ddx(cot−1(x))=−11+x2\begin{aligned} cot(y) &= x \\ -csc^2(y) \cdot \frac{dy}{dx} &= 1 \quad \textit{(Implicit Differentiation)} \\ \frac{dy}{dx} &= -\frac{1}{csc^2(y)} \\ \frac{dy}{dx} &= -\frac{1}{1 + cot^2(y)} \\ \frac{d}{dx}(cot^{-1}(x)) &= -\frac{1}{1 + x^2} \\ \end{aligned}

Derivative of Inverse Secant Function

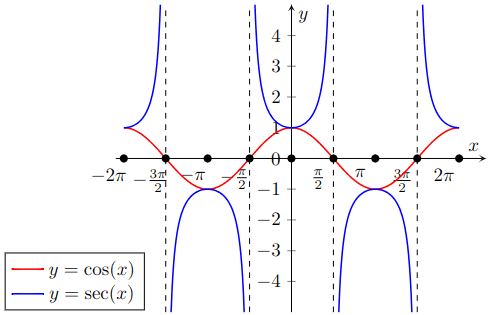
ddx(sec−1(x))=1∣x∣⋅x2−1\frac{d}{dx}(sec^{-1}(x)) = \frac{1}{\lvert x \rvert \cdot \sqrt{x^2 - 1}}
Graph of y=sec(x)y = sec(x) and y=cos(x)y = cos(x)

cos sec plot

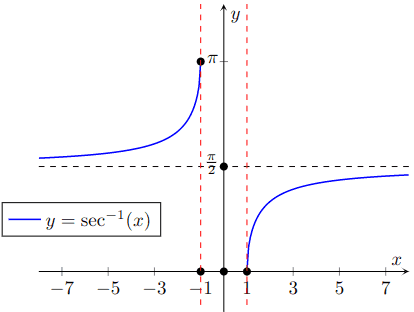
Graph of y=sec−1(x)y = sec^{-1}(x)

inverse sec plot

Proof
y=sec−1(x)sec(y)=xddx(sec(y))=ddx(x)sec(y)⋅tan⁡(y)⋅dydx=1dydx=1sec(y)⋅tan⁡(y) ,tan(y)=±x2−1\begin{aligned} y &= sec^{-1}(x) \\[10pt] sec(y) &= x \\[10pt] \frac{d}{dx}(sec(y)) &= \frac{d}{dx}(x) \\[10pt] sec(y) \cdot \tan(y) \cdot \frac{dy}{dx} &= 1 \\[10pt] \frac{dy}{dx} &= \frac{1}{sec(y) \cdot \tan(y)} \text{ ,} \quad tan(y) = \pm\sqrt{x^2 - 1} \\[10pt] \end{aligned}

(Note: tan2(y)+1=sec2(y)  ⟹  tan2(y)=sec2(y)−1=x2−1tan^2(y) + 1 = sec^2(y) \implies tan^2(y) = sec^2(y) - 1 = x^2 - 1)

Case 1: y=sec−1(x)y = sec^{-1}(x), x≥1x \geq 1, y∈[0,π2)y \in [0, \frac{\pi}{2})
dydx=1sec(y)⋅tan⁡(y)=1x⋅x2−1 , x>1\begin{aligned} \frac{dy}{dx} &= \frac{1}{sec(y) \cdot \tan(y)} \\ &= \frac{1}{x \cdot \sqrt{x^2 - 1}} \text{ , } x > 1 \\ \end{aligned}
Case 2: y=sec−1(x)y = sec^{-1}(x), x≤−1x \leq -1, y∈(π2,π]y \in (\frac{\pi}{2}, \pi]
dydx=1sec(y)⋅tan⁡(y)=1x⋅−x2−1 , x<−1\begin{aligned} \frac{dy}{dx} &= \frac{1}{sec(y) \cdot \tan(y)} \\ &= \frac{1}{x \cdot -\sqrt{x^2 - 1}} \text{ , } x < -1 \\ \end{aligned}
Conclusion
dydx=1x⋅x2−1 , x>1dydx=1−x⋅x2−1 , x<−1}  ⟹  dydx=1∣x∣⋅x2−1 , x>1 or x<−1\begin{aligned} \begin{rcases} \frac{dy}{dx} = \frac{1}{ x \cdot \sqrt{x^2 - 1}} \text{ , } x > 1 \\ \frac{dy}{dx} = \frac{1}{-x \cdot \sqrt{x^2 - 1}} \text{ , } x < -1 \\ \end{rcases} \implies \frac{dy}{dx} = \frac{1}{\lvert x \rvert \cdot \sqrt{x^2 - 1}} \text{ , } x > 1 \text{ or } x < -1 \end{aligned}

Derivative of Inverse Cosecant Function

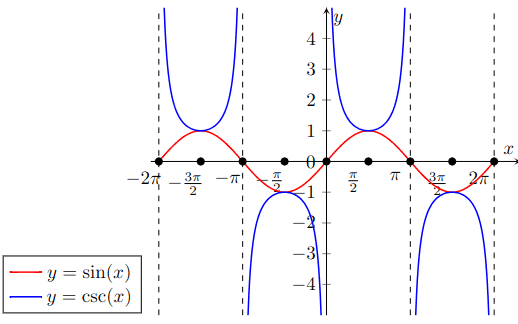
ddx(csc−1(x))=−1∣x∣⋅x2−1\frac{d}{dx}(csc^{-1}(x)) = -\frac{1}{\lvert x \rvert \cdot \sqrt{x^2 - 1}}
Graph of y=csc(x)y = csc(x) and y=sin(x)y = sin(x)

sin csc plot

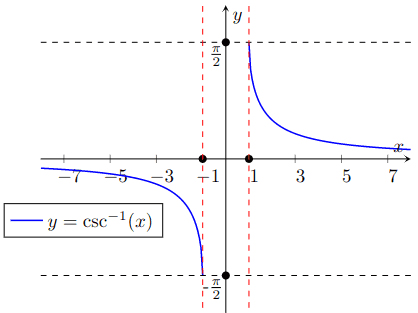
Graph of y=csc−1(x)y = csc^{-1}(x)

inverse csc plot

Proof
y=csc−1(x)csc(y)=xddx(csc(y))=ddx(x)−csc(y)⋅cot⁡(y)⋅dydx=1dydx=−1csc(y)⋅cot⁡(y) ,cot(y)=±x2−1\begin{aligned} y &= csc^{-1}(x) \\[10pt] csc(y) &= x \\[10pt] \frac{d}{dx}(csc(y)) &= \frac{d}{dx}(x) \\[10pt] -csc(y) \cdot \cot(y) \cdot \frac{dy}{dx} &= 1 \\[10pt] \frac{dy}{dx} &= -\frac{1}{csc(y) \cdot \cot(y)} \text{ ,} \quad cot(y) = \pm\sqrt{x^2 - 1} \\[10pt] \end{aligned}

(Note: 1+cot2(y)=csc2(y)  ⟹  cot2(y)=csc2(y)−1=x2−11 + cot^2(y) = csc^2(y) \implies cot^2(y) = csc^2(y) - 1 = x^2 - 1)

Case 1: y=csc−1(x)y = csc^{-1}(x), x≥1x \geq 1, y∈(0,π2]y \in (0, \frac{\pi}{2}]
dydx=−1csc(y)⋅cot⁡(y)=−1x⋅x2−1 , x>1\begin{aligned} \frac{dy}{dx} &= -\frac{1}{csc(y) \cdot \cot(y)} \\[10pt] &= -\frac{1}{x \cdot \sqrt{x^2 - 1}} \text{ , } x > 1 \\[10pt] \end{aligned}
Case 2: y=csc−1(x)y = csc^{-1}(x), x≤−1x \leq -1, y∈[−π2,0)y \in [-\frac{\pi}{2}, 0)
dydx=−1csc(y)⋅cot⁡(y)=−1x⋅−x2−1 , x<−1\begin{aligned} \frac{dy}{dx} &= -\frac{1}{csc(y) \cdot \cot(y)} \\ &= -\frac{1}{x \cdot -\sqrt{x^2 - 1}} \text{ , } x < -1 \\ \end{aligned}
Conclusion
dydx=−1x⋅x2−1 , x>1dydx=−1−x⋅x2−1 , x<−1}  ⟹  dydx=−1∣x∣⋅x2−1 , x>1 or x<−1\begin{aligned} \begin{rcases} \frac{dy}{dx} = -\frac{1}{ x \cdot \sqrt{x^2 - 1}} \text{ , } x > 1 \\[10pt] \frac{dy}{dx} = -\frac{1}{-x \cdot \sqrt{x^2 - 1}} \text{ , } x < -1 \\[10pt] \end{rcases} \implies \frac{dy}{dx} = -\frac{1}{\lvert x \rvert \cdot \sqrt{x^2 - 1}} \text{ , } x > 1 \text{ or } x < -1 \end{aligned}

Antiderivative and The Fundamental Theorem of Calculus

If f(x)f(x) is continuous on [a,b][a, b] then F(x)=∫axf(t)dtF(x) = \int_{a}^{x} f(t)dt, a≤x≤ba \leq x \leq b. F(x)F(x) is continuous on [a,b][a, b] and differentiable on (a,b)(a, b). F′(x)=f(x)F'(x) = f(x), that means F(x)F(x) the antiderivative of f(x)f(x)

Conclusion

The Fundamental Theorem of Calculus is one of the key theorems in Calculus hence we need to know the definition of antiderivative. Also, I have shown you how to derivative the common model. Thank you for reading and see you soon.

Profile picture

Written by Gapry, 魏秋
Twitter | GitHub | Facebook | Mastodon