Use Derivative to Find the Extreme Values

Introduction

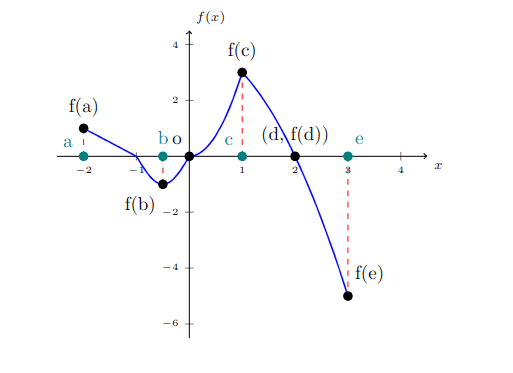
I use the graph to show you what is the meaning of extreme value.

Suppose $x \in [-2, 3]$

• $f(e)$ is the global minimum value, $x \in [-2, 3]$.
• $f(c)$ is the global maximum value, $x \in [-2, 3]$.
• $f(b)$ is the local minimum value, $x \in [-1, 0]$.
• $f(a)$ is the local maximum value, $x \in [-2, 0]$.

Definition: Global Extreme Value

Let $c$ $\in$ $D$, $D$ is the Domain of the function $f$.

• If $f(c) \geq f(x)$, $\forall x \in D$, then $f(c)$ is the global maximum value.
• If $f(c) \leq f(x)$, $\forall x \in D$, then $f(c)$ is the global minimum value.

Definition: Local Extreme Value

Let $c$ $\in$ $S$, $D$ is the Domain of the function $f$ and $S \subset D$.

• If $f(c) \geq f(x)$, $\forall x \in S$, then $f(c)$ is the local maximum value.
• If $f(c) \leq f(x)$, $\forall x \in S$, then $f(c)$ is the local minimum value.

The Extreme Value Theorem

$f$ is continuous on $[a, b] \in R \Rightarrow$ it exists the global extreme values of $f$.

Fermat’s Theorem

$f$ has a local extremum at $x = c$ $\Rightarrow$ $f'(c) = 0$ or $f'(c)$ does not exist.

Proof

Let $h > 0$ or $h < 0$, Then

Case 1. $h > 0$

Case 2. $h < 0$

If $f'(c) \geq 0$ and $f'(c) \leq 0$, $f'(c) = 0$ must be true.

Definition: Critical Point

If $c$ is a critical point of $f$ $\Leftrightarrow$ $f'(c) = 0$ or $f'(c)$ does not exist.

Algorithm: Find the Global Extreme Value

1. Find the derivative of the function $f$, $f$ in $[a, b]$
2. Find all critical points using $f'(x) = 0$
3. Evaluate the values of $f$ at all critical points
4. Evaluate the values of $f$ at all endpoints
5. Compare the evaluated values and get the extreme values